Support Vector Machines (SVM)

SVM: sélection de fonctionnalités et noyaux

Une machine à vecteur de support (SVM) est un algorithme d'apprentissage automatique supervisé qui peut être utilisé à des fins de classification et de régression. (Noel Bambrick.)

Introduction

Support Vector Machines (SVM) est un algorithme d'apprentissage machine qui peut être utilisé pour de nombreuses tâches différentes (figure 1). Dans cet article, je vais expliquer la base mathématique pour démontrer comment cet algorithme fonctionne à des fins de classification binaire.

Figure 1: Applications SVM

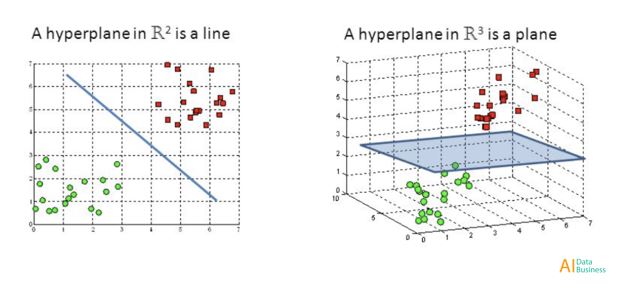
L'objectif principal dans SVM est de trouver l'hyperplan optimal pour classer correctement entre les points de données de différentes classes (figure 2). La dimensionnalité de l'hyperplan est égale au nombre d'entités en entrée moins un (par exemple. Lorsque vous travaillez avec trois entités, l'hyperplan sera un plan bidimensionnel).

Figure 2: Hyperplan SVM

Les points de données d'un côté de l'hyperplan seront classés dans une certaine classe tandis que les points de données de l'autre côté de l'hyperplan seront classés dans une classe différente (par exemple, vert et rouge comme sur la figure 2). La distance entre l'hyperplan et le premier point (pour toutes les différentes classes) de chaque côté de l'hyperplan est une mesure sûre que l'algorithme concerne sa décision de classification. Plus la distance est grande et plus nous pouvons être confiants, SVM prend la bonne décision.

Les points de données les plus proches de l'hyperplan sont appelés vecteurs de support. Les vecteurs de support déterminent l'orientation et la position de l'hyperplan, afin de maximiser la marge du classificateur (et donc le score de classification). Le nombre de vecteurs de support que l'algorithme SVM doit utiliser peut être choisi arbitrairement en fonction des applications.

La classification SVM de base peut être facilement implémentée à l'aide de la bibliothèque Scikit-Learn Python en quelques lignes de code.

Il existe deux principaux types d'algorithmes de classification SVM Marge dure et Marge souple:

Marge dure: vise à trouver le meilleur hyperplan sans tolérer aucune forme de mauvaise classification.
Marge souple: nous ajoutons un degré de tolérance dans SVM. De cette façon, nous permettons au modèle de classer volontairement quelques points de données si cela peut conduire à identifier un hyperplan capable de généraliser mieux les données invisibles.

Soft Margin SVM peut être implémenté dans Scikit-Learn en ajoutant un terme de pénalité C dans svm.SVC. Plus C est élevé et plus l'algorithme est pénalisé lors d'une erreur de classification.

Astuce du noyau

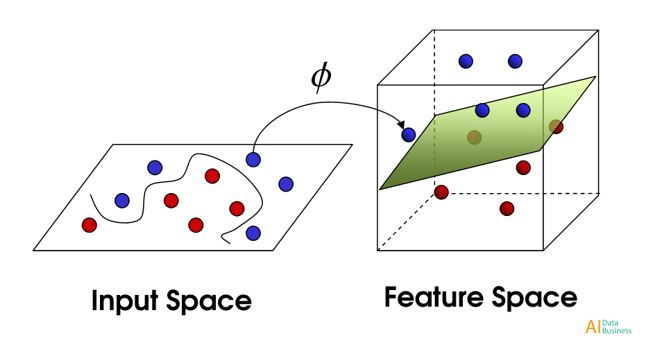
Si les données avec lesquelles nous travaillons ne sont pas séparables linéairement (conduisant ainsi à de mauvais résultats de classification SVM linéaire), il est possible d'appliquer une technique connue sous le nom de Kernel Trick. Cette méthode est capable de cartographier nos données séparables non linéaires dans un espace de dimension supérieure, ce qui rend nos données séparables linéairement. L'utilisation de ce nouvel espace dimensionnel SVM peut alors être facilement implémentée (figure 3). 
 

Figure 3: noyau

Il existe de nombreux types de noyaux différents qui peuvent être utilisés pour créer cet espace de dimension supérieure, certains exemples sont la fonction de base linéaire, polynomiale, sigmoïde et radiale (RBF). Dans Scikit-Learn, une fonction de noyau peut être spécifiée en ajoutant un paramètre de noyau dans svm.SVC. Un paramètre supplémentaire appelé gamma peut être inclus pour spécifier l'influence du noyau sur le modèle.

Il est généralement suggéré d'utiliser des noyaux linéaires si le nombre d'entités est supérieur au nombre d'observations dans l'ensemble de données (sinon RBF pourrait être un meilleur choix).

Lorsque vous travaillez avec une grande quantité de données à l'aide de RBF, la vitesse peut devenir une contrainte à prendre en compte.

Sélection de fonctionnalité

Une fois notre SVM linéaire ajusté, il est possible d'accéder aux coefficients du classificateur à l'aide  .coef_du modèle entraîné. Ces poids représentent les coordonnées vectorielles orthogonales orthogonales à l'hyperplan. Leur direction représente plutôt la classe prédite.

L'importance des caractéristiques peut donc être déterminée en comparant la taille de ces coefficients les uns aux autres. En examinant les coefficients SVM, il est donc possible d'identifier les principales caractéristiques utilisées dans la classification et de se débarrasser de celles qui ne sont pas importantes (qui contiennent moins de variance).

La réduction du nombre de fonctionnalités dans Machine Learning joue un rôle très important, en particulier lorsque vous travaillez avec de grands ensembles de données. Cela peut en effet: accélérer la formation, éviter le surapprentissage et finalement conduire à de meilleurs résultats de classement grâce à la réduction du bruit dans les données.

Bibliographie

[1] Support Vector Machine without tears, Ankit Sharma. Consulté à: https://www.slideshare.net/ankitksharma/svm-37753690

[2] Support Vector Machine — Introduction to Machine Learning Algorithms, Rohith Gandhi. Consulté sur: https://towardsdatascience.com/support-vector-machine-introduction-to-machine-learning-algorithms-934a444fca47